A coordinate system is "a way to define locations in space", typically using numbers or coordinates. It’s an arrangement of lines or curves that define the position of points or other geometric elements in space. The most commonly used coordinate systems are the Cartesian system and the polar system.
Cartesian Coordinate System
The Cartesian (Rectangular) system uses perpendicular lines (axes) to define a point’s location.
-
\(\mathbb{R} = \{x: x \in \mathbb{R}\}\) - the number line.
-
\(\mathbb{R}^2 = \{(x,y): x,y \in \mathbb{R}\}\) - two-dimensional Cartesian plane.
-
\(\mathbb{R}^3 = \{(x,y,z): x,y,z \in \mathbb{R}\}\) - three-dimensional Cartesian space.
-
\(\mathbb{R}^n = \{(x_1, x_2, \dots, x_n): x_i \in \mathbb{R}, i=1,\dots, n\}\) - \(n-\) dimensional cartesian space. This is an abstract space.
Example 01:
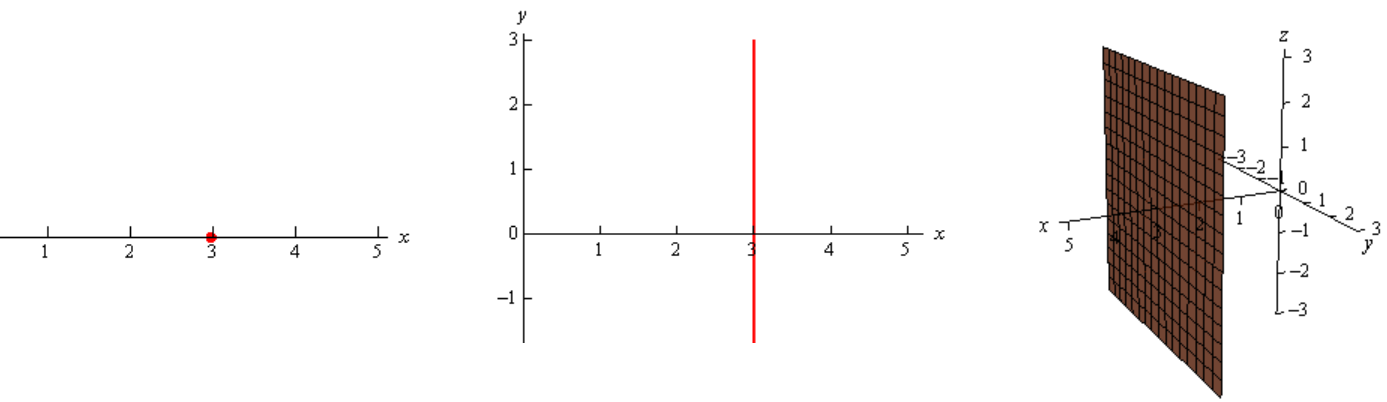
Plot \(x=3\) in \(\mathbb{R}, \mathbb{R}^2, \mathbb{R}^3\):
-
In \(\mathbb{R}\), it’s a point.
-
In \(\mathbb{R}^2\), the equation tells us to graph all the points that are in the form \((3,y)\): it’s a vertical line.
-
In \(\mathbb{R}^3\), the equation tells us to graph all the points that are in the form \((3,y,z)\): it’s a plane. This is a plane that is parallel to the \(yz\)-plane and passes through the \(x\)-axis at \(x=3\).
Example 02:
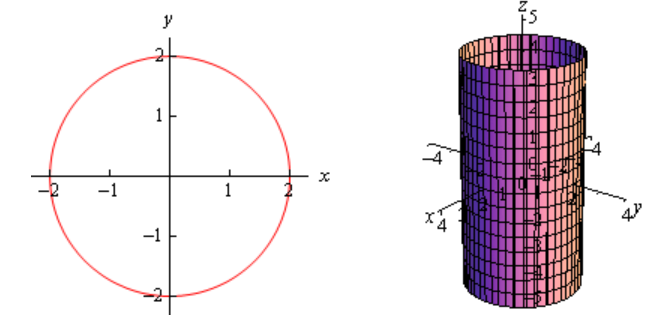
Plot \(x^2+y^2=4\) in \(\mathbb{R}^2\) and \(\mathbb{R}^3\):
-
In \(\mathbb{R}^2\), this is a circle centered at the origin with radius 2.
-
In \(\mathbb{R}^3\), this may or may not be a circle. Since we have not specified \(z\) in any way we must assume that \(z\) can take on any value. In other words, at any value of \(z\) this equation must be satisfied and so at any value \(z\) we have a circle of radius 2 centered on the \(z\)-axis. This means that we have a cylinder of radius 2 centered on the \(z\)-axis.
Polar Coordinate System
The polar system uses a distance from the origin and an angle to define a point’s location. In the Cartesian system, we defined a point by starting at the origin and then moving \(x\) units horizontally followed by \(y\) units vertically.
This is not, however, the only way to define a point in two dimensional space. Instead of moving vertically and horizontally from the origin to get to the point we could instead go straight out of the origin until we hit the point and then determine the angle this line makes with the positive \(x\)-axis.
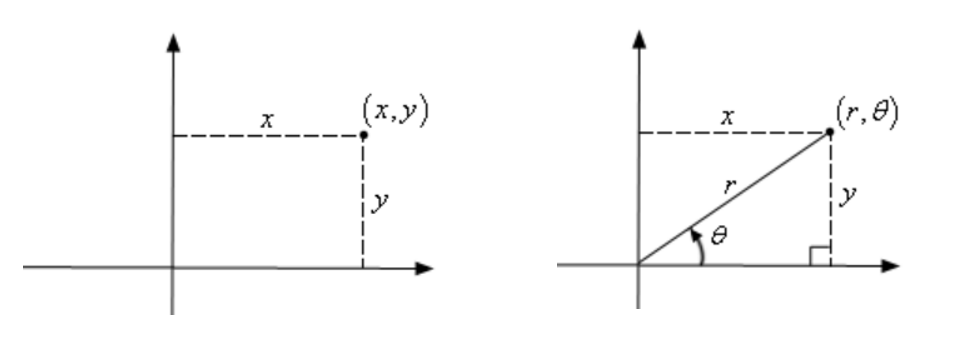
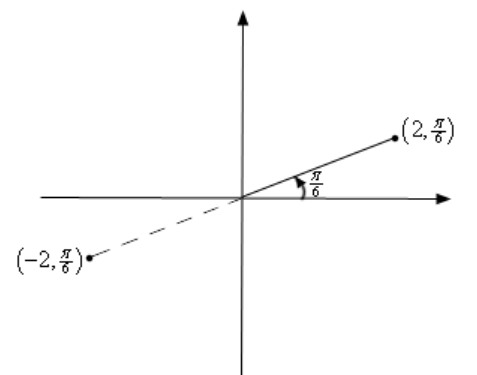
We could then use the distance of the point from the origin and the amount we needed to rotate from the positive \(x\)-axis as the coordinates of the point \((r,\theta)\). The co-ordinates in this form are called polar co-ordinates. \(r\) can be negative as well. Below is the sketch of the points \((2,\frac{\pi}{6})\) and \((-2,\frac{\pi}{6})\). Here \(\frac{\pi}{6}\) is in radians.
There is an important difference between Cartesian coordinates and polar coordinates. In Cartesian coordinates there is exactly one set of coordinates for any given point. With polar coordinates this isn’t true. In polar coordinates there is literally an infinite number of coordinates for a given point. For example, the following four coordinates correspond to the same point:
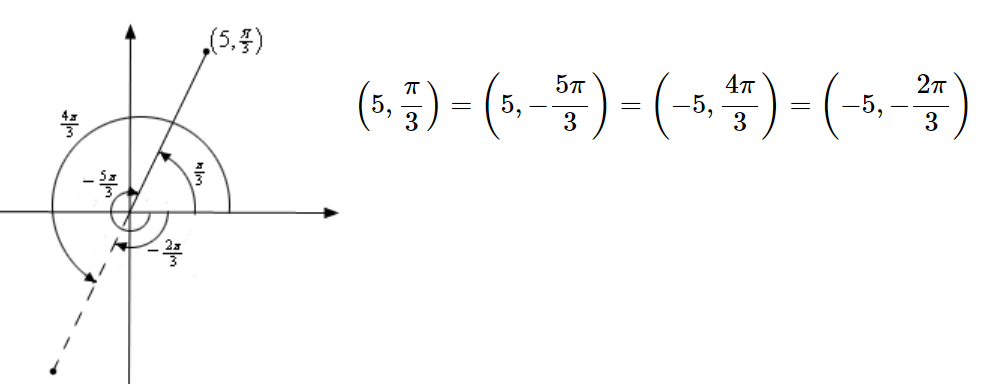
|
Note
|
Moving out in the opposite quadrant is indicated with a negative sign for \(r\). Rotation in clockwise direction is indicated with a negative sign for \(\theta\). |
The coordinates are obtained by \((5,\frac{\pi}{3}) = (5, -2\pi + \frac{\pi}{3}) = (-5,\frac{\pi}{3} + \pi) = (-5,\frac{\pi}{3} - \pi)\).
To plot \((5, \frac{\pi}{3})\):
-
Start from the positive \(x\)-axis, rotate \(\frac{\pi}{3}\) anti-clockwise and then move out a distance of 5 in the same quadrant where it ends, \((5, \frac{\pi}{3})\).
-
Start from the positive \(x\)-axis, rotate \(\frac{5\pi}{3}\) clockwise and then move out a distance of 5 in the same quadrant where it ends, \((5, -\frac{5\pi}{3})\).
These four points only represent the coordinates of the point without rotating around the system more than once. If we allow the angle to make as many complete rotations as we want, then there are an infinite number of coordinates for the same point.
A point \((r,\theta)\) can be represented by any of the following co-ordinate pairs:
where \(n\) is any integer (\(n=0, \pm 1, \pm2, \dots\)).
|
Caution
|
In polar coordinates, the origin is often called the pole. \(r\) will be 0 but we can still rotate around the system by any angle we want, so the coordinates of the origin/pole are \((0,\theta)\). |
We just saw the polar coordinate system in a two-dimensional structure. But it can also be extended to three dimensions in two ways: the cylindrical coordinate system adds a second distance coordinate, and the spherical coordinate system adds a second angular coordinate.
Conversion between Coordinate Systems
Let’s focus on converting 2D Cartesian coordinates into 2D polar coordinates, and vice versa.
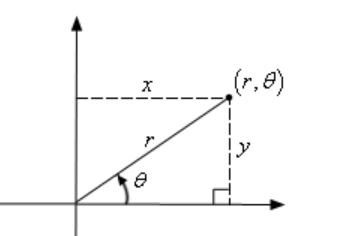
Cartesian to Polar:
Consider we have a point in space represented by Cartesian coordinates \((x,y)\). To represent the same point in the polar coordinate system:
So, \(r = \sqrt{x^2 + y^2}\). Note that technically we should have a plus or minus in front of the root since we know that \(r\) can be either positive or negative. We will run with the convention of positive \(r\) here.
For \(\theta\):
The domain of \(\tan^{-1}\) is \(\mathbb{R}\) and the range is \((-\frac{\pi}{2}, \frac{\pi}{2})\). The inverse tangents only return values in the range \((-\frac{\pi}{2}, \frac{\pi}{2})\). But recall that there is a second possible angle which results in the same value and it is given by \(\theta + \pi\).
Polar to Cartesian:
Consider we have a point in space represented by polar coordinates \((r,\theta)\). To represent the same point in the Cartesian coordinate system:
References
-
[Paul] Dawkins, Paul. Pauls online notes. Lamar University. Retrieved May 9, 2025, from https://tutorial.math.lamar.edu/

