Can a simple neural network really model any Boolean function? While a single-layer perceptron struggles with non-linearly separable problems like XOR, a multi-layer perceptron (MLP) breaks through these limitations - making it a universal Boolean function approximator!
Shortcomings of Perceptrons
The Perceptron algorithm requires data to be linearly separable for convergence. However, some datasets cannot be separated by a single hyperplane. A classic example is the XOR function, which is not linearly separable. If we attempt to implement XOR using a single perceptron:

There exist no values of \(w_0, w_1, w_2\) that satisfy the conditions required to correctly classify all points. This demonstrates why a single-layer perceptron cannot model the XOR function. Let’s increase the number of perceptrons.
Multi-Layer Perceptrons (MLP)
To overcome this limitation, we can connect multiple perceptrons in a networked structure, forming a Multi-Layer Perceptron (MLP). Unlike a single perceptron, an MLP can learn non-linear decision boundaries, allowing it to model complex functions such as XOR.
Consider an MLP with five perceptrons, configured as follows:
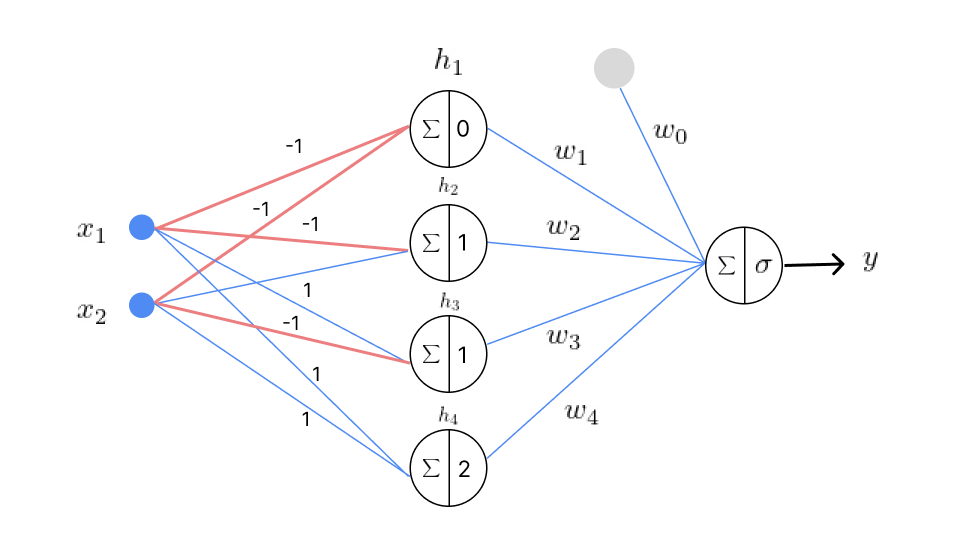
Each perceptron in this network activates for one specific input pattern, producing the following outputs:
-
For \(x_1=0, x_2=0\), the output \(\mathbf{h}\) is \((1,0,0,0)\).
-
For \(x_1=0, x_2=1\), the output \(\mathbf{h}\) is \((0,1,0,0)\).
-
For \(x_1=1, x_2=0\), the output \(\mathbf{h}\) is \((0,0,1,0)\).
-
For \(x_1=1, x_2=1\), the output \(\mathbf{h}\) is \((0,0,0,1)\).
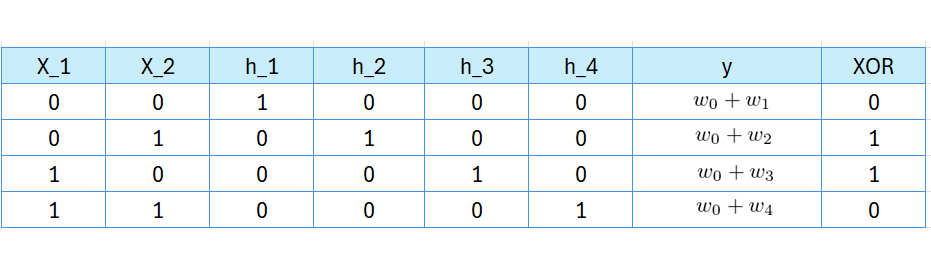
To correctly classify XOR, the network must satisfy the following conditions:
Unlike a single perceptron, these conditions do not conflict and can be satisfied. This confirms that an MLP can successfully model the XOR function, demonstrating the power of multi-layer networks in learning non-linearly separable patterns.
MLP as a Universal Boolean Function Approximator
A Multi-Layer Perceptron (MLP) is capable of realizing any Boolean function, meaning that for any given Boolean function, there exists at least one MLP configuration that can represent it. However, this result does not specify the required depth of the network.
In general, any Boolean function with \(N\) inputs can be exactly represented using \(2^N\) perceptrons in the hidden layer and one perceptron in the output layer.
Universal AND Function
Consider a Boolean function with three input variables: \(f(X_1, X_2, X_3) = X_1X_2\bar{X}_3\). This function can be modeled using the following network:
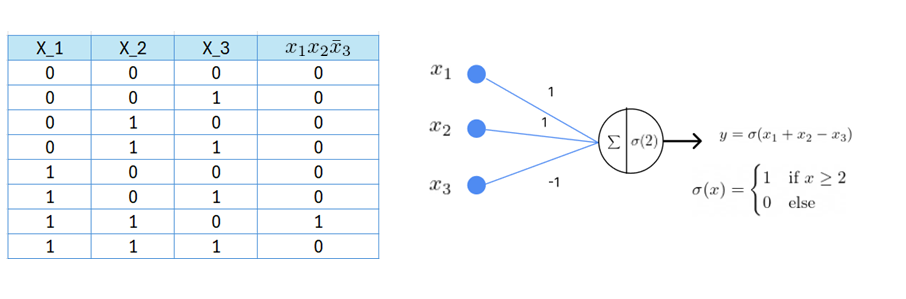
In general, any AND function of \(N\) variables
can be modelled using a single perceptron with the following configuration
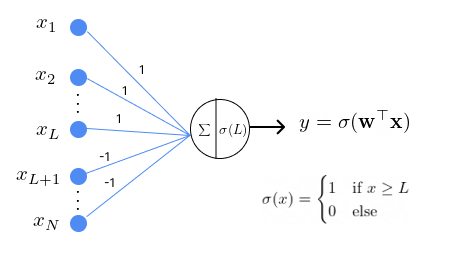
where the weights for inputs \(x_1, \dots, x_L\) are set to 1 and the weights for inputs \(x_{L+1}, \dots, x_N\) are set to -1. The threshold is \(L\).
Universal OR Function
Similarly, any OR function of \(N\) variables
can be modelled using a single perceptron with the following configuration
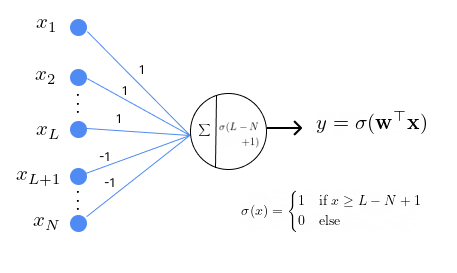
where the weights for inputs \(x_1, \dots, x_L\) are set to 1 and the weights for inputs \(x_{L+1}, \dots, x_N\) are set to -1. The threshold is \(L-N+1\).
Since all Boolean functions can be expressed in terms of AND, OR, and NOT operations, we can use these two networks to model any Boolean function.
Example: Modeling a Boolean Function
Consider the following Boolean function:
-
Each term can be represented by a single perceptron using an AND operation in the hidden layer.
-
A final output perceptron combines all hidden layer outputs using an OR operation to compute \(f(x_1, x_2, x_3, x_4)\).
This approach demonstrates that any truth table can be represented in this manner, making a one-hidden-layer MLP a universal Boolean function approximator.
Number of Neurons Required
What is the maximum number of perceptrons required in the (single) hidden layer to model an \(N\)-input Boolean function?
We have seen that any Boolean function of N inputs can be represented with at most \(2^N + 1\) perceptrons However, this approach is inefficient, as the hidden layer size grows exponentially. In this configuration, each hidden neuron independently handles a specific input-output scenario, with no cooperation between neurons.
While \(2^N + 1\) neurons are sufficient to represent any Boolean function, they are not necessary - we can often use fewer neurons through simplifications.
Simplification using Karnaugh Maps
Using a Karnaugh map, we can simplify Boolean expressions. For example:
Karnaugh maps represent truth tables as grids, where adjacent 1s can be grouped together, reducing complexity. After simplification, the MLP can be configured based on the reduced Boolean expression, significantly reducing the required number of neurons.
Worst-Case Scenario: When Reduction is Not Possible
If the arrangement of 1s and 0s in the Karnaugh map does not allow for further grouping, the Boolean function remains complex. For example, consider a function with four input variables where the Karnaugh map is:
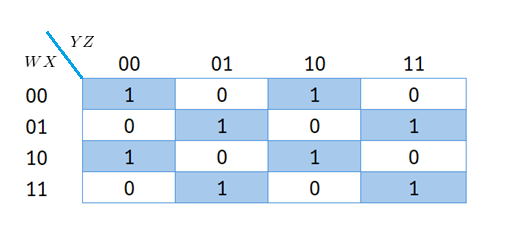
In this case, no adjacent cells can be grouped, meaning the Boolean function requires eight terms: \(\bar{W}\bar{X}\bar{Y}\bar{Z} + \bar{W}\bar{X}\bar{Y}Z + \dots + WXYZ\)
This implies that modeling a Boolean function of four variables requires a maximum of 8 neurons in the hidden layer and 1 in the output layer.
In general, for an \(N\)-input Boolean function, we need a maximum of \(2^{N-1}\) neurons in the (single) hidden layer and one neuron in the output layer.
|
Note
|
The number of neurons required reduces significantly when we increase the number of layers. |
Optimizing the XOR Function
Previously, we modeled the XOR function using 4 neurons in the hidden layer. However, we can reduce this to just 2 neurons. The Karnaugh map for XOR is
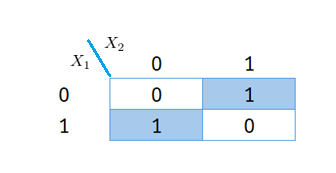
The simplified Boolean expression for XOR is: \(f(X_1, X_2) = \bar{X}_1X_2 + X_1\bar{X}_2\). This function can be efficiently modeled using: one perceptron for each term in the hidden layer and one perceptron in the output layer to perform the final OR operation.
Conclusion
-
MLPs can model any Boolean function, making them universal Boolean function approximators.
-
The number of required neurons depends on Boolean complexity, but optimizations (such as Karnaugh maps) can drastically reduce network size.
-
Deep networks (more than one hidden layer) require fewer neurons than wide, single-hidden-layer networks, making them more efficient.
References
-
CMU School of Computer Science. See https://www.cs.cmu.edu/~bhiksha/courses/deeplearning/Spring.2018/www/slides/lec2.universal.pdf

